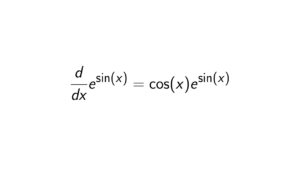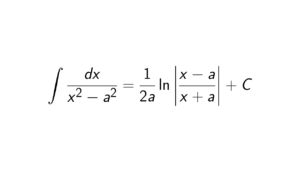How to calculate polynomials over GF(2)

An important topic in coding theory is how to calculate polynomials over the field

GF(2)

. In this article, we will see what precisely such a polynomial over

GF(2)

is and how to calculate polynomials in the mod (for example,

f(x)

mod

g(x)

What is a polynomial over GF(2)?

A polynomial of degree

n

over

GF(2)

is a polynomial

f(x) = a_{0} + a_{1}x^{1} + \dots + a_{n}x^{n}

with

a_{0} \ldots a_{n} \in {0,1}

. The set of all polynomials over

GF(2)

is denoted as

GF(2)[x]

.

Example.

f(x) = 1 + x^2

where

a_{0} = a_{2} = 1

, and

g(x) = 1 + x + x^2

where

a_{0} = a_{1} = a_{2} = 1

Now we are going to the point which you probably came for. How do we calculate

f(x)

modulo

g(x)

? We will give some examples.

Example. Let

f(x) = 1 + x + x^{7}

, and

g(x) = x^5

. Then

\begin{equation*} 1 + x + x^7 \text{ mod } g(x) \equiv 1 + x + x^2 \end{equation*}

So far it looks easy. We only replaced the

x^7 \text{ mod } x^5 \equiv x^2

. Now we will get to another example:

Example. Let

f(x) = 1 + x^4 + x^{5}

, and

g(x) = 1 + x + x^3

. Then

\begin{align*} 1 + x^4 + x^5 \text{ mod } g(x) & \equiv 1 + x^3 x + x^3 x^2 \text{ mod } g(x) \\ & \equiv 1 + (1 + x) x + (1 + x) x^2 \text{ mod } g(x) \\ & \equiv 1 + x + x^2 + x^2 + x^3 \text{ mod } g(x) \\ & \equiv 1 + x + 2x^2 + (1 + x) \text{ mod } g(x) \\ & \equiv 0 \end{align*}

So what did we do above exactly? For each

x^3

, we replace that with

1 + x

, since

x^3 = x + 1

is in

GF(2)[x]

. Now a question for you: can you figure out why

x + x^2 + x^3 + x^6 \text{ mod } 1 + x + x^4 \equiv x