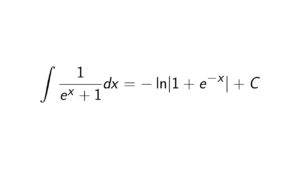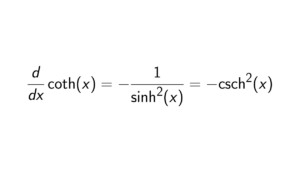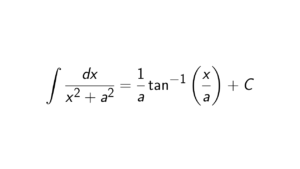Proof. Since we need to look at degrees at least 3, we can take (12),(13) \in S_n. Now note that:
\begin{align*}
(12)(13) = (132)
\end{align*}\begin{align*}
(13)(12) = (123).
\end{align*}\begin{align*}
(12)(13) = (132) \neq (123) = (13)(12).
\end{align*}