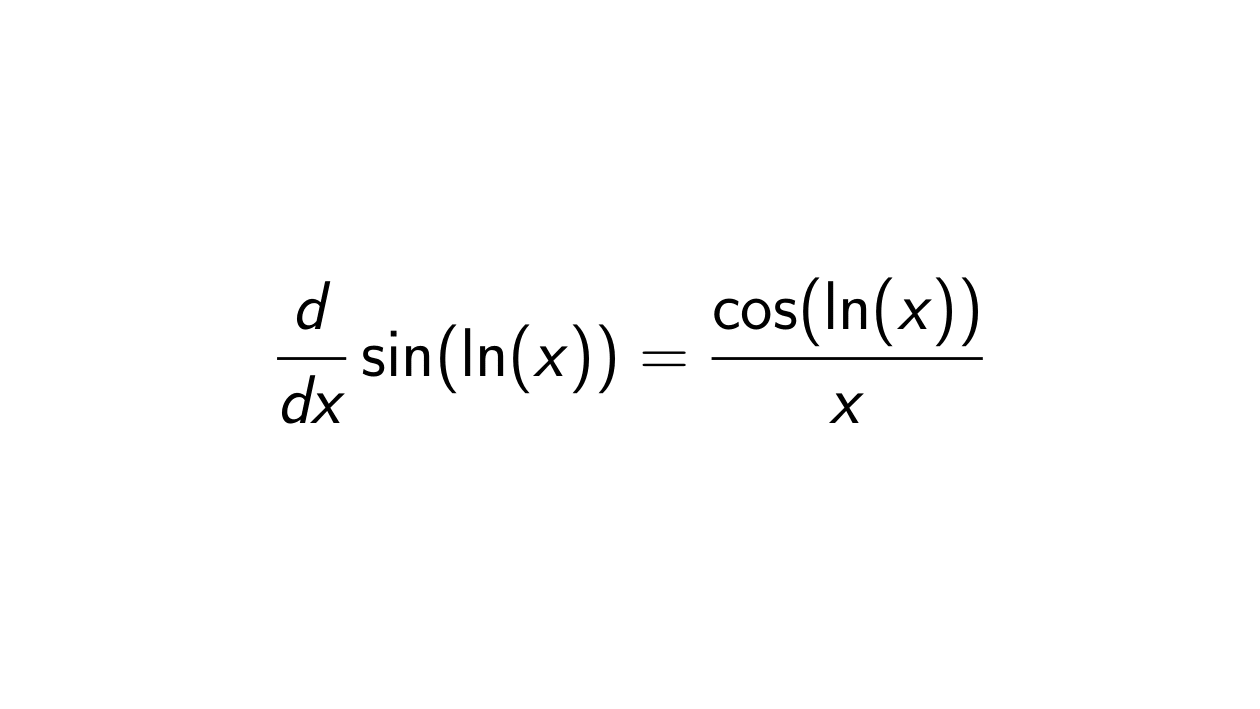Solution. To determine the derivative F(x) = f(g(x)) = \sin(\ln(x)), we will use the chain rule:
\begin{align*}
F'(x) = f'(g(x))g'(x),
\end{align*}\begin{align*}
f'(g(x)) = \cos(g(x)) = \cos(\ln(x)).
\end{align*}\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= \cos(\ln(x))\frac{1}{x} \\
&= \frac{\cos(\ln(x))}{x}.
\end{align*}