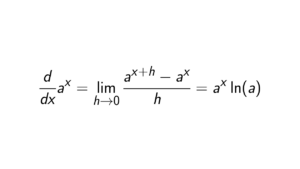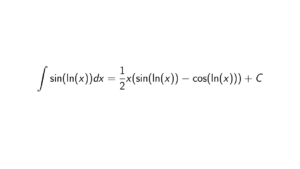Blog

Let $R$ be a commutative ring with identity $1 \neq 0$. The ideal $M$ of $R$ is maximal iff the quotient ring $R/M$ is a field.

Proof. This proof can be easily done by using the Lattice Isomorphism Theorem of Rings.

“$\Rightarrow$“: Given maximal ideal $M$ of $R$. By the Lattice Isomorphism Theorem of Rings, the ideals of $R$ containing $M$ correspond bijectively with the ideals of $R/M$. The only ideals of $R$ that consist $M$ are $M$ and $R$ itself. So we have that $R/R \cong 0$ and $R/M$ are ideals of $R/M$. We use a handy proposition which we have proven here which implies that $R/M$ is a field.

“$\Leftarrow$“: Given $R/M$ a field. Then by this proposition here, we have that the only ideals of $R/M$ are $0$ and $R/M$. We use the Lattice Isomorphism Theorem of Rings again, which means that there are two ideals consisting $M$. We know that at least it is $M$ and $R$, which is already two. This implies there is no ideal $I$ of $R$ such that $M \subset I \subset R$. Therefore, $M$ is a maximal ideal of $R$.