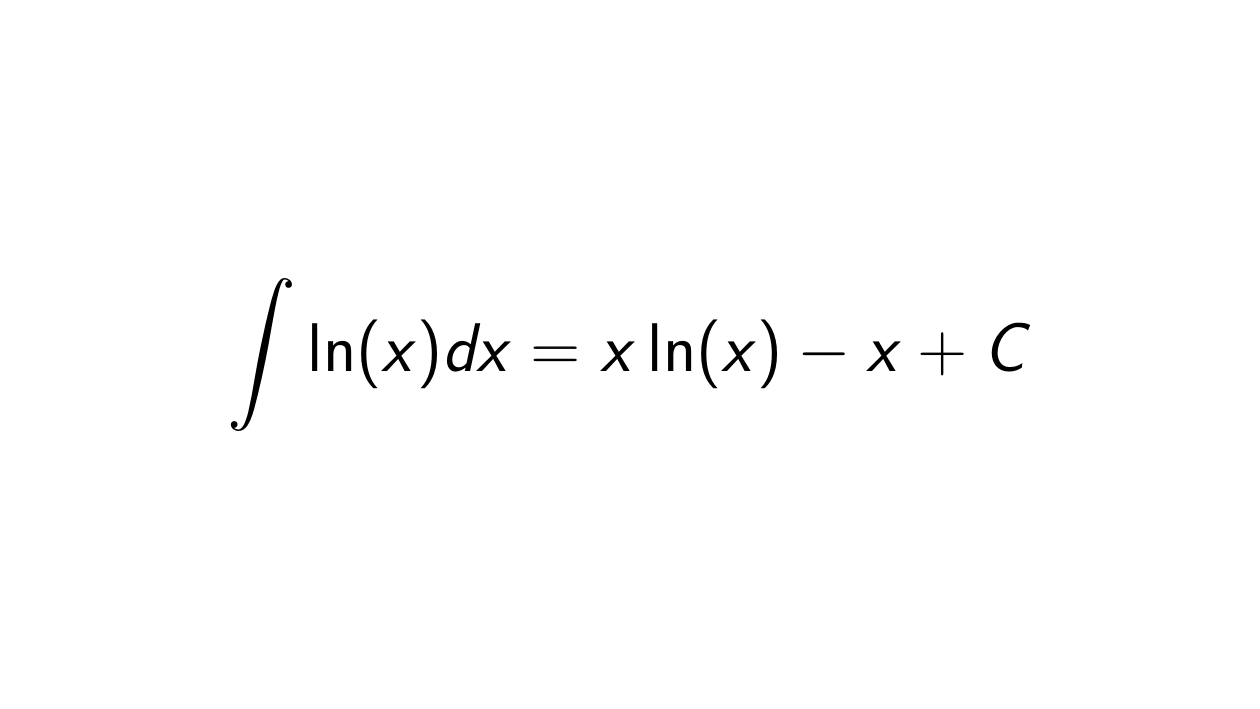Solution. We want to determine the integral of \ln(x):
\begin{align*}
\int \ln(x) dx.
\end{align*}\begin{align*}
\int UdV = UV - \int VdU,
\end{align*}\begin{align*}
U = \ln(x), \quad &dV = dx\\
dU = \frac{1}{x}dx, \quad &V = x.
\end{align*}\begin{align*}
\int \ln(x) dx &= x\ln(x) - \int x \cdot \frac{1}{x} dx \\
&= x \ln(x) - \int dx \\
&= x \ln(x) - x + C.
\end{align*}