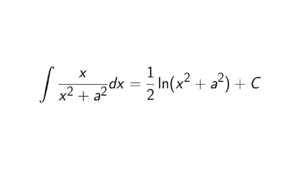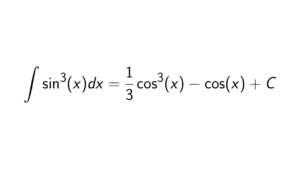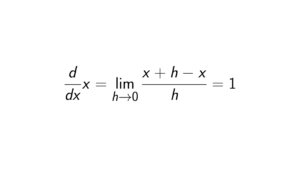Prove that the rings \mathbb{Z}[x] and \mathbb{Q}[x] are not isomorphic.
This question can be tackled in many different ways. Depending on your ring theory knowledge, we will introduce two clever ways to prove this.
Proof 1. We can check the units of \mathbb{Z}[x] and \mathbb{Q}[x]. We know that \mathbb{Z}[x]^{\times} = \{\pm 1\} and \mathbb{Q}[x]^{\times} = \mathbb{Q}^{\times}. Both have a whole different structure w.r.t. to the units.
Proof 2. The ideal (2,x) is not a principal ideal of \mathbb{Z}[x], so \mathbb{Z}[x] is not a principal ideal domain. But \mathbb{Q}[x] is a principal ideal domain since \mathbb{Q} is a field.