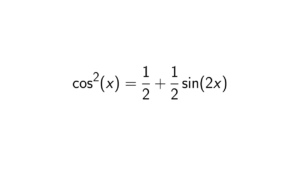Matrix ring is not commutative for dimensions greater or equal to 2

If $R$ is any nontrivial ring and $n \geq 2$ , then $M_n(R)$ is not commutative.

Proof. For simplicity, we start with

n = 2

. Let

A,B \in M_n(R)

such that

A = \begin{pmatrix} r_{11} & 0 \\ 0 & 0 \end{pmatrix} \text{ and } \begin{pmatrix} 0 & r_{12} \\ 0 & 0 \end{pmatrix}

where

r_{11}r_{12} \neq 0

and

r_{12}r_{11} \neq 0

and

r_{11},r_{12} \in R

. Multiplying the matrices

A

and

B

gives us:

AB = \begin{pmatrix} r_{11} & 0 \\ 0 & 0 \end{pmatrix}\begin{pmatrix} 0 & r_{12} \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & r_{11}r_{12} \\ 0 & 0 \end{pmatrix}

and

BA = \begin{pmatrix} 0 & r_{12} \\ 0 & 0 \end{pmatrix}\begin{pmatrix} r_{11} & 0 \\ 0 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 0 & 0 \end{pmatrix}.

So we see that

AB \neq BA

. So, the matrix ring is not commutative for dimension 2.

Now, we take dimension

n \geq 3

. Let

A

be a matrix where the coefficient

r_{11} \in R

is the first row and first column position of

A

and zero elsewhere. Further, let

B

be a matrix where the coefficient

r_{12} \in R

is the first row and second column position of

B

and zero elsewhere. Let

r_{11}r_{12} \neq 0

and

r_{12}r_{11} \neq 0

. Then if we multiply

A

and

B

, then for

AB

, we have on the first row and second column position the value

r_{11}r_{12}

and zero everywhere, and for

BA

, we have everywhere zero. This proves that

AB \neq BA

, and therefore, the matrix ring is not commutative for dimensions greater or equal than 2.