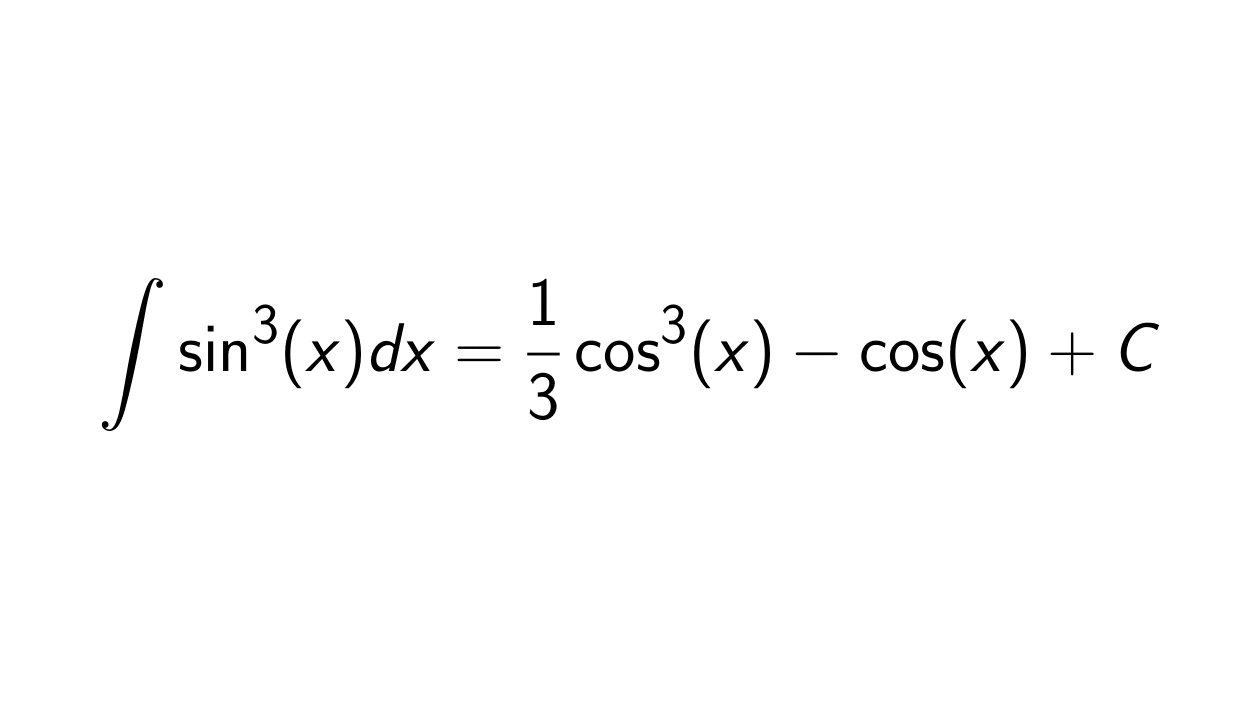What is the integral of sin^3(x)?

integral of sin^3(x)

The integral of

\sin^3(x)

\frac{1}{3}\cos^3(x) - \cos(x) + C

.

Solution. We want to determine the integral of

\sin^3(x)

, that is:

\begin{align*} \int \sin^3(x) dx. \end{align*}

Notice that we have seen here that

\sin^2(x) = 1 - \cos^2(x)

. So we get:

\begin{align*} \int \sin^3(x) dx = \int \sin^2(x)\sin(x) dx = \int (1 - \cos^2(x))\sin(x) dx. \end{align*}

We will apply the substitution method. Let

u = \cos(x)

, then we saw here that

dU = -\sin(x)dx

. Therefore, we get the following:

\begin{align*} \int (1 - \cos^2(x))\sin(x) dx &= -\int (1 - u^2) du \\ &= -u + \frac{1}{3}u^3 + C \\ &= -\cos(x) + \frac{1}{3} \cos^3(x) + C. \end{align*}

Therefore, the integral of

\sin^3(x)

\frac{1}{3}\cos^3(x) - \cos(x) + C