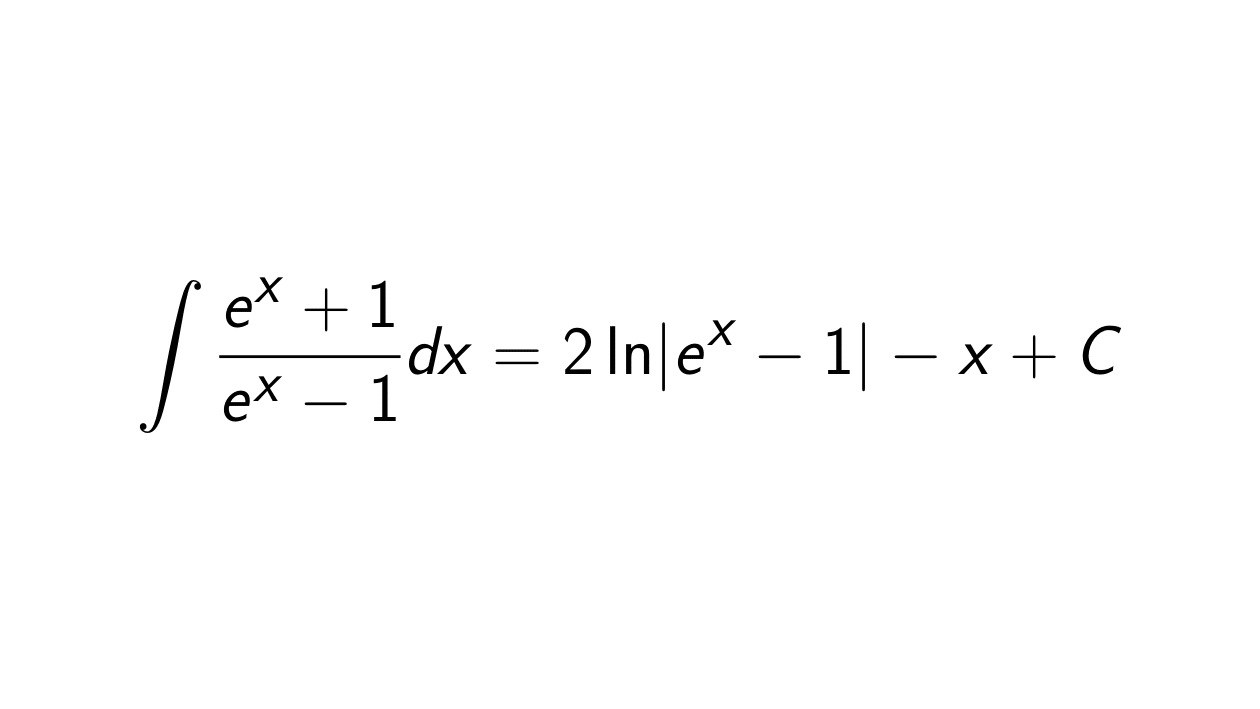The integral of
ex−1ex+1 is
2ln∣ex−1∣−x+C.
Solution. We want to determine the integral of
ex−1ex+1, i.e.:
∫ex−1ex+1dx=∫ex−1exdx+∫ex−11dx.
First we will determine
∫ex−1exdx. We will use the substitution method. So take
u=ex−1. Then we saw
here that
du=exdx. Therefore, we get the following:
∫ex−1exdx=∫udu=ln∣u∣+C1=ln∣ex−1∣+C1,
where
C1 is some constant. Now what is left is to determine
∫ex−11dx. This integral is difficult to determine, but we make it easy by using the following handy adjustment:
∫ex−11dx=∫ex(1−e−x)1dx=∫1−e−xe−xdx.
Now we will apply the substitution method. Let
v=1−e−x. Then we saw
here that
dv=e−xdx. So we get the following:
∫1−e−xe−xdx=∫vdv=ln∣v∣+C2=ln∣1−e−x∣+C2=ln∣e−x(ex−1)∣+C2=ln∣e−x∣+∣e−x−1∣+C2=−x+∣e−x−1∣+C2,
where
C2 is some constant. Now we will combine everything together:
∫ex−1ex+1dx=∫ex−1exdx+∫ex−11dx=ln∣ex−1∣+C1−x+∣e−x−1∣+C2=2ln∣ex−1∣−x+C,
where
C=C1+C2. So, the integral of
ex−1ex+1 is
2ln∣ex−1∣−x+C.