Proof. We have seen here that:
\begin{align*}
\sin^2(x) + \cos^2(x) = 1.
\end{align*}\begin{align*}
\frac{\sin^2(x)}{\cos^2(x)} + 1 = \frac{1}{\cos^2(x)}.
\end{align*}\begin{align*}
\tan^2(x) + 1 = \sec^2(x).
\end{align*}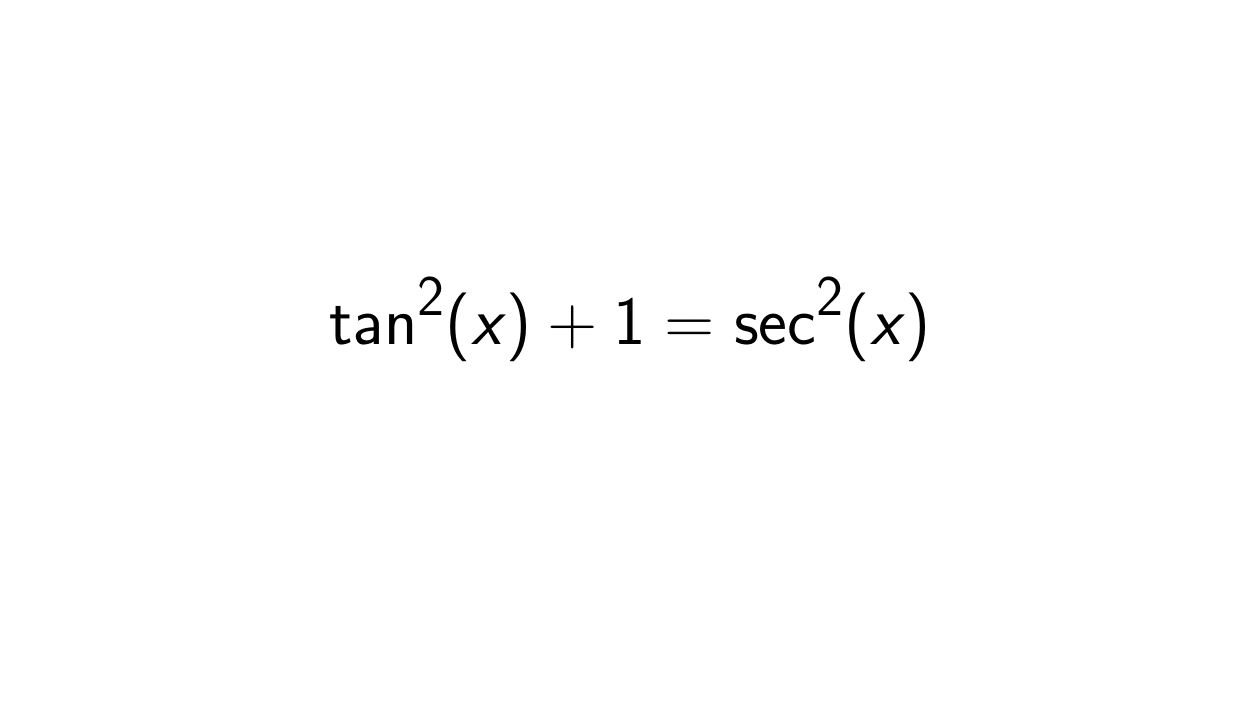
\begin{align*}
\sin^2(x) + \cos^2(x) = 1.
\end{align*}\begin{align*}
\frac{\sin^2(x)}{\cos^2(x)} + 1 = \frac{1}{\cos^2(x)}.
\end{align*}\begin{align*}
\tan^2(x) + 1 = \sec^2(x).
\end{align*}