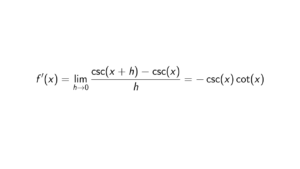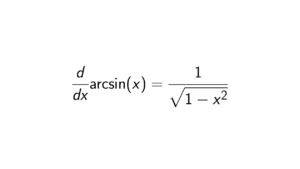Proof. To find the generators, it suffices for us to check whether for an element a \in \mathbb{Z}/48\mathbb{Z} that gcd(a,48) = 1. In other words, we need to determine the elements of (\mathbb{Z}/48\mathbb{Z})^{\times}, where its cardinality is 16. Obviously, 1 is the generator of \mathbb{Z}/48\mathbb{Z}. Notice that \lvert \mathbb{Z}/48\mathbb{Z} \rvert = 48, and 48 = 2^4 3. So we do know that all even elements less or equal to 47 and primes 2 and 3 are not generators. All primes equal to 47 or less are generators of \mathbb{Z}/48\mathbb{Z}:
\begin{align*}
5,7,11,13,17,19,23,29,31,37,41, \text{ and } 47.
\end{align*}\begin{align*}
9,15,21,25,27,33,35,39, \text{ and } 45.
\end{align*}\begin{align*}
1,5,7,11,13,17,19,23,25,29,31,35,37,41,45, \text{ and } 47.
\end{align*}