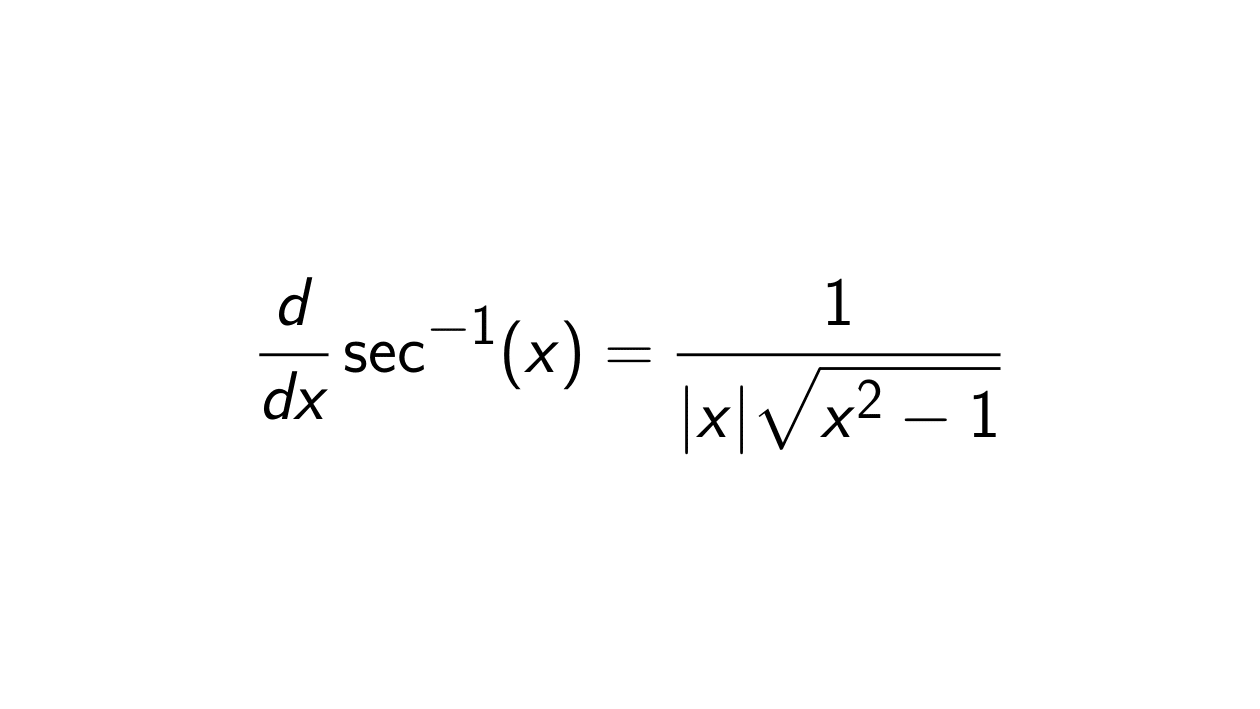What is the Derivative of arcsec(x)?

The derivative of

\text{arcsec}(x)

\frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}

.

Solution. Let

F(x) = \sec^{-1}(x) = \text{arcsec}(x)

with

\lvert x \rvert \geq 1

. We have seen here that

\begin{align*} F(x) = \sec^{-1}(x) = \cos^{-1}(1/x). \end{align*}

Now let

f(u) = \cos^{-1}(u)

and

g(x) = 1/x

such that

F(x) = f(g(x))

. To determine the derivative

\sec^{-1}

, we neet to use the chain rule:

\begin{align*} F'(x) = f'(g(x))g'(x). \end{align*}

We know from here that:

\begin{align*} f'(u) = \frac{d}{du} \cos^{-1}(u) = \frac{-1}{\sqrt{1 - u^2}} \end{align*}

and from here that:

\begin{align*} g'(x) = -\frac{1}{x^2}. \end{align*}

So we get:

\begin{align*} f'(g(x)) = \frac{-1}{\sqrt{1 - g(x)^2}} = \frac{-1}{\sqrt{1 - \frac{1}{x^2}}}. \end{align*}

Combining everything, we get:

\begin{align*} F'(x) &= f'(g(x))g'(x) \\ &= \frac{-1}{\sqrt{1 - \frac{1}{x^2}}} \Bigg(-\frac{1}{x^2}\Bigg) \\ &= \frac{1}{x^2} \frac{1}{\sqrt{1 - \frac{1}{x^2}}} \\ &= \frac{1}{x^2} \frac{1}{\sqrt{\frac{x^2 - 1}{x^2}}} \\ &= \frac{1}{x^2} \frac{\sqrt{x^2}}{\sqrt{x^2 - 1}} \\ &= \frac{1}{x^2} \frac{\lvert x \rvert}{\sqrt{x^2 - 1}} \\ &= \frac{1}{\lvert x \rvert} \frac{1}{\sqrt{x^2 - 1}} \\ &= \frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}. \end{align*}

Therefore we get:

\begin{align*} F'(x) = \frac{d}{dx} \text{arcsec}(x) = \frac{d}{dx} \sec^{-1}(x) = \frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}. \end{align*}

So, the derivative of

\text{arcsec}(x)

\frac{1}{\lvert x \rvert \sqrt{x^2 - 1}}