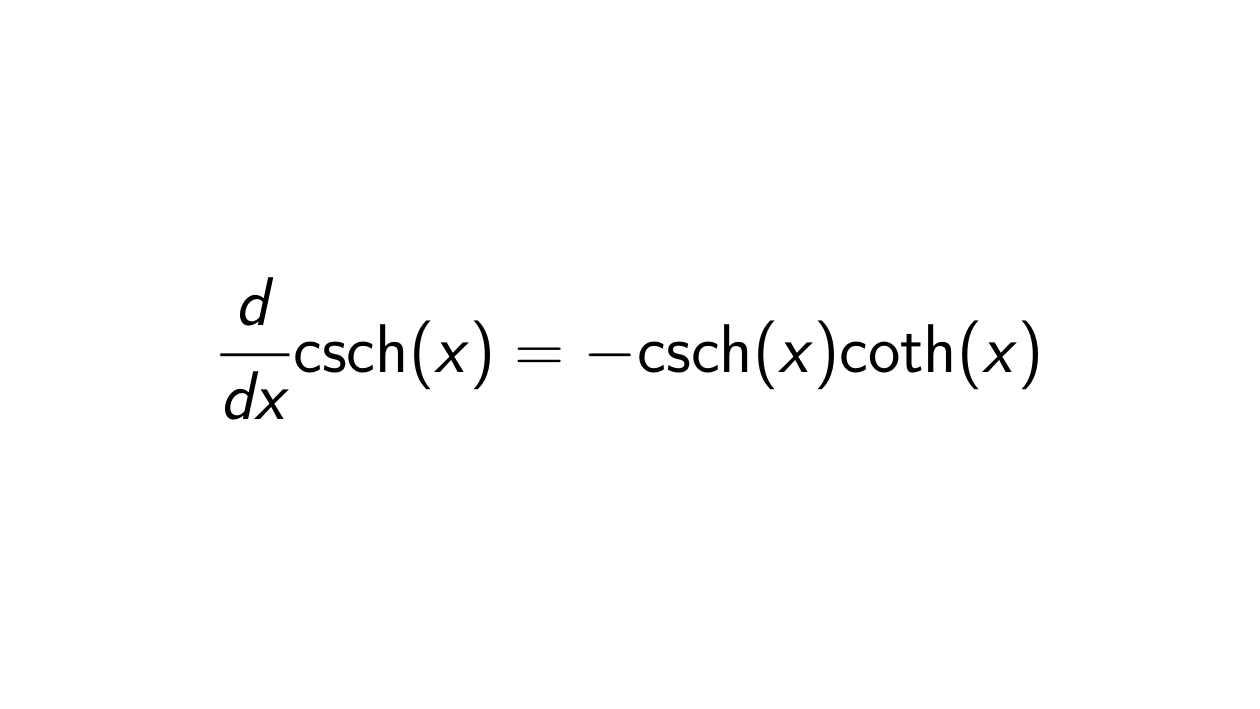What is the Derivative of Hyperbolic Cosecant?

Derivative of csch(x)

The derivative of

\text{csch}(x)

-\text{csch}(x)\text{coth}(x)

.

Solution. Let

F(x) = \text{csch}(x) = \frac{2}{e^x - e^{-x}}

where

f(u) = \frac{2}{u}

and

g(x) = e^x - e^{-x}

such that

F(x) = f(g(x))

. Then we will use the chain rule to find the derivative of

\text{csch}(x)

\begin{align*} F'(x) = f'(g(x))g'(x). \end{align*}

We know from here that

g'(x) = e^x + e^{-x}

and that

f'(u) = \frac{-2}{u^2}

. So we get:

\begin{align*} f'(g(x)) = \frac{-2}{g(x)^2} = \frac{-2}{(e^x + e^{-x})^2}. \end{align*}

So, substituting everything, we get:

\begin{align*} F'(x) &= f'(g(x))g'(x) \\ &= \frac{-2}{(e^x - e^{-x})^2} \cdot (e^x + e^{-x}) \\ &= \frac{-2(e^x + e^{-x})}{(e^x - e^{-x})^2} \\ &= \frac{-2}{e^x - e^{-x}} \cdot \text{coth}(x) \\ &= - \text{csch}(x)\text{coth}(x). \end{align*}

So, the derivative of

\text{csch}(x)

-\text{csch}(x)\text{coth}(x)