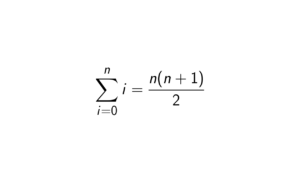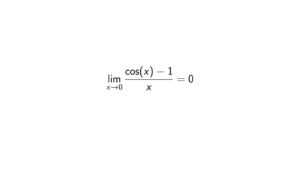Proof. Let f(x) = a^x. Note that a^x = e^{x\ln(a)}. Then
\begin{align*}
f'(x) &= \lim_{h \rightarrow 0} \frac{f(x + h) - f(x)}{h} \\
&= \lim_{h \rightarrow 0} \frac{a^{x + h} - a^x}{h} \\
&= \lim_{h \rightarrow 0} \frac{e^{(x+h)\ln(a)} - e^{x\ln(a)}}{h} \\
&= \lim_{h \rightarrow 0} \frac{e^{x\ln(a)}(e^{h\ln(a)} - 1)}{h} \\
&= e^{x\ln(a)} \cdot \lim_{h \rightarrow 0} \frac{e^{h\ln(a)} - 1}{h} \\
&= a^x \cdot \lim_{h \rightarrow 0} \frac{e^{h\ln(a)} - 1}{h}.
\end{align*}\begin{align*}
\lim_{h \rightarrow 0} \frac{e^{h\ln(a)} - 1}{h},
\end{align*}\begin{align*}
e^x &= \sum_{n = 0}^{\infty} \frac{x^n}{n!} \\
&= 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots
\end{align*}\begin{align*}
e^{h\ln(a)} &= \sum_{n = 0}^{\infty} \frac{(h\ln(a))^n}{n!} \\
&= 1 + h\ln(a) + \frac{(h\ln(a))^2}{2!} + \frac{(h\ln(a))^3}{3!} + \cdots
\end{align*}\begin{align*}
e^{h\ln(a)} - 1 &= \sum_{n = 1}^{\infty} \frac{(h\ln(a))^n}{n!} \\
&= h\ln(a) + \frac{(h\ln(a))^2}{2!} + \frac{(h\ln(a))^3}{3!} + \cdots.
\end{align*}\begin{align*}
\frac{e^{h\ln(a)} - 1}{h} &= \sum_{n = 1}^{\infty} \frac{h^{n-1}\ln(a)^n}{n!} \\
&= \ln(a) + \frac{h\ln(a)^2}{2!} + \frac{h^2\ln(a)^3}{3!} + \cdots
\end{align*}\begin{align*}
\lim_{h \rightarrow 0} \frac{e^{h\ln(a)} - 1}{h} &= \lim_{h \rightarrow 0} \sum_{n = 1}^{\infty} \frac{h^{n-1}\ln(a)^n}{n!} \\
&= \lim_{x \rightarrow 0} \bigg(\ln(a) + \frac{h\ln(a)^2}{2!} + \frac{h^2\ln(a)^3}{3!} + \cdots\bigg) \\
&= \ln(a) + \lim_{x \rightarrow 0} \bigg(\frac{h\ln(a)^2}{2!} + \frac{h^2\ln(a)^3}{3!} + \cdots\bigg) \\
&= \ln(a) + 0 + 0 + 0 + \cdots \\
&= \ln(a).
\end{align*}\begin{align*}
f'(x) = a^x \cdot \lim_{h \rightarrow 0} \frac{e^{h\ln(a)} - 1}{h} = a^x \ln(a).
\end{align*}