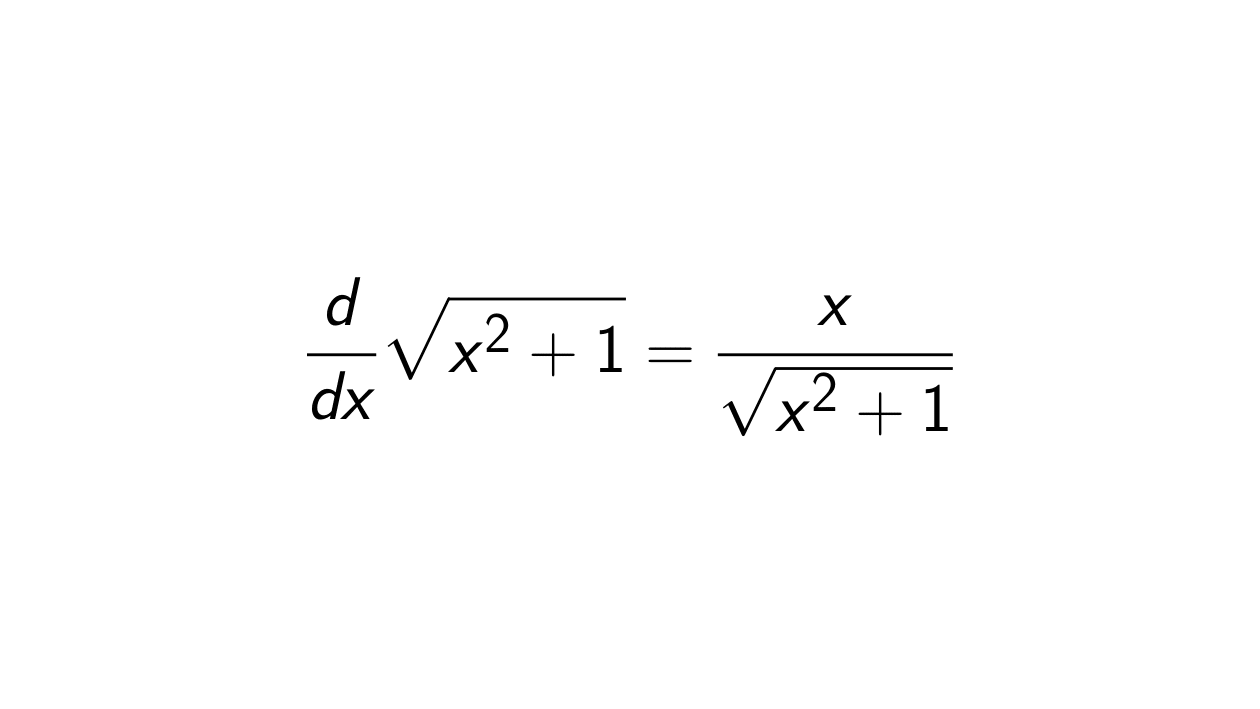Solution. Let F(x) = \sqrt{x^2 + 1}, f(u) = \sqrt{u} = u^{\frac{1}{2}} and g(x) = x^2 + 1 such that F(x) = f(g(x)). Using the chain rule, we can find the derivative of \sqrt{x^2 + 1}:
\begin{align*}
F'(x) = f'(g(x))g'(x).
\end{align*}\begin{align*}
f'(g(x)) = \frac{1}{2\sqrt{x^2 + 1}}.
\end{align*}\begin{align*}
F'(x) &= f'(g(x))g'(x) \\
&= \frac{1}{2\sqrt{x^2 + 1}} \cdot 2x \\
&= \frac{x}{\sqrt{x^2 + 1}}.
\end{align*}