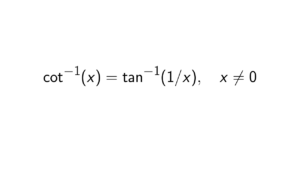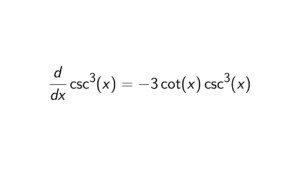Proof. We need to prove that if p divides n, then p-1 divides the Euler’s totient function of n. Assume that p \mid n. Then n = p^{\alpha}c for some integer c and positive integer \alpha where p doesn’t divide c. Now since p \nmid c, this implies that gcd(p^{\alpha},c) = 1. Since the Euler’s totient function is multiplicative, we can apply that \phi(p^{\alpha}c) = \phi(p^{\alpha})\phi(c). So together, we get
\begin{align*}
\phi(n) &= \phi(p^{\alpha}c) \quad \quad \text{ since } n = p^{\alpha}c \\
&=\phi(p^m)\phi(c) \quad \text{ since } gcd(p^{\alpha},c) = 1 \\
&= p^{\alpha - 1}(p-1)\phi(c).
\end{align*}