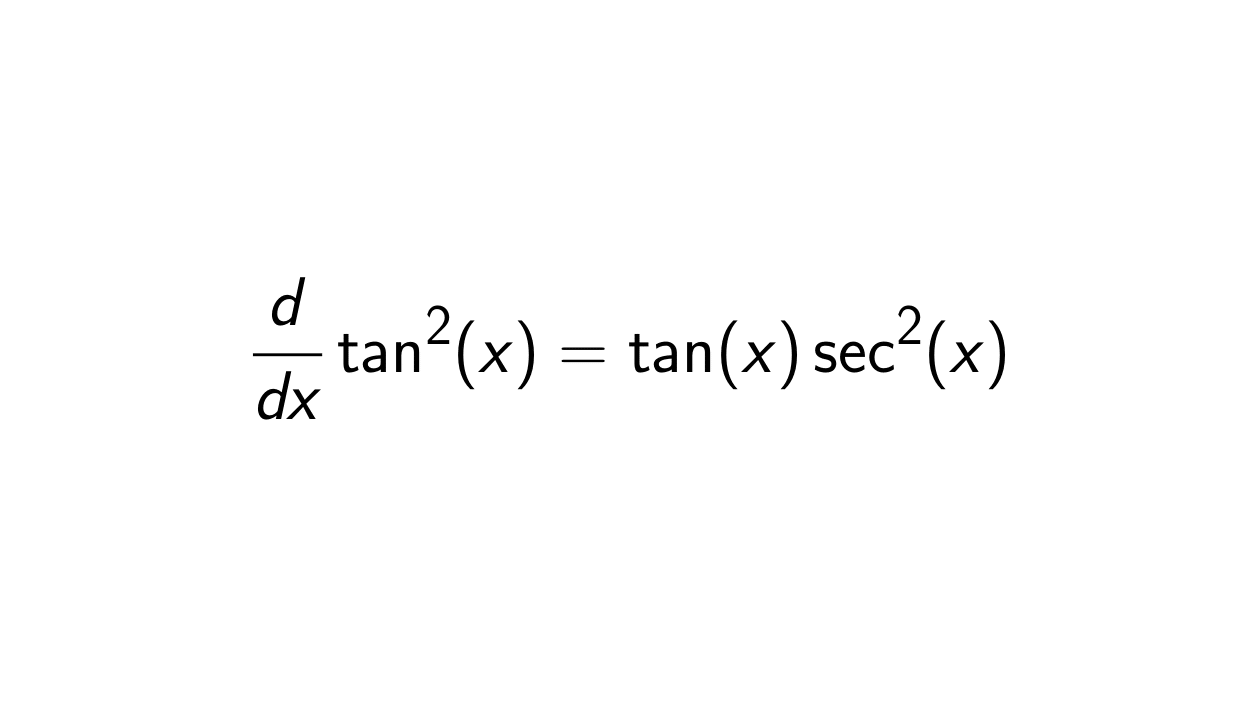What is the derivative of tan^2(x)?

derivative of tan^2(x)

We will determine the derivative of

\tan^2(x)

.

Proof. Let

F(x) = \tan^2(x)

f(u) = u^2

and

g(x) = \tan(x)

such that

F(x) = f(g(x))

. We can use the chain rule

\begin{align*} F'(x) = f'(g(x))g'(x). \end{align*}

We know that

\frac{d}{dx}\tan(x) = \sec^2(x)

f'(u) = 2u

. Therefore:

\begin{align*} f'(g(x)) = 2g(x) = 2\tan(x) \quad \text{and} \quad g'(x) = \sec^2(x). \end{align*}

Combining everything, we get:

\begin{align*} F(x) &= f'(g(x))g'(x) \\ &= 2\tan(x)\sec^2(x). \end{align*}

which completes the proof. So the derivative of

\tan^2(x)

2\tan(x)\sec^2(x)