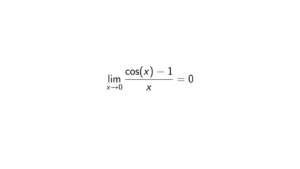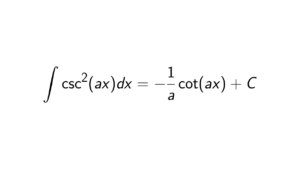- \cosh(x+y) = \cosh(x)\cosh(y) + \sinh(x)\sinh(y)
- \sinh(x+y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)
- \tanh(x + y) = \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}.
\begin{align*}
\sinh(x) = \frac{e^x - e^{-x}}{2}, \quad \cosh(x) = \frac{e^x + e^{-x}}{2}, \quad \tanh(x) = \frac{\sinh(x)}{\cosh(x)} = \frac{e^x - e^{-x}}{e^x + e^{-x}}.
\end{align*}\begin{align*}
\cosh(x)\cosh(y) + \sinh(x)\sinh(y) &= \frac{e^x + e^{-x}}{2} \cdot \frac{e^y - e^{-y}}{2} + \frac{e^x - e^{-x}}{2}\cdot \frac{e^y - e^{-y}}{2} \\
&= \frac{1}{4}(e^{x+y} + e^{x - y} + e^{-x + y} + e^{-x-y}) \ + \\ & \ \quad \frac{1}{4}(e^{x+y} - e^{x - y} - e^{-x + y} + e^{-x-y}) \\
&= \frac{1}{2}(e^{x + y} + e^{-x-y}) \\
&= \cosh(x+y)
\end{align*}\begin{align*}
\sinh(x)\cosh(y) + \cosh(x)\sinh(y) &= \frac{e^x - e^{-x}}{2} \cdot \frac{e^y + e^{-y}}{2} + \frac{e^x + e^{-x}}{2}\cdot \frac{e^y - e^{-y}}{2} \\
&= \frac{1}{4}(e^{x+y} + e^{x - y} - e^{-x + y} - e^{-x-y}) \ + \\ & \ \quad \frac{1}{4}(e^{x+y} - e^{x - y} + e^{-x + y} - e^{-x-y}) \\
&= \frac{1}{2}(e^{x + y} - e^{-x-y}) \\
&= \sinh(x+y)
\end{align*}\begin{align*}
\tanh(x + y) &= \frac{\sinh(x + y)}{\cosh(x + y)} \\
&= \frac{\sinh(x)\cosh(y) + \cosh(x)\sinh(y)}{\cosh(x)\cosh(y) + \sinh(x)\sinh(y)} \\
&= \frac{\sinh(x)\cosh(y) + \cosh(x)\sinh(y)}{\cosh(x)\cosh(y) + \sinh(x)\sinh(y)} \cdot \frac{\frac{1}{\cosh(x)\cosh(y)}}{\frac{1}{\cosh(x)\cosh(y)}} \\
&= \frac{\frac{\sinh(x)\cosh(y)}{\cosh(x)\cosh(y)} + \frac{\cosh(x)\sinh(y)}{\cosh(x)\cosh(y)}}{\frac{\cosh(x)\cosh(y)}{\cosh(x)\cosh(y)} + \frac{\sinh(x)\sinh(y)}{\cosh(x)\cosh(y)}} \\
&= \frac{\frac{\sinh(x)}{\cosh(x)} + \frac{\sinh(y)}{\cosh(y)}}{1 + \frac{\sinh(x)}{\cosh(x)}\cdot\frac{\sinh(y)}{\cosh(y)}} \\
&= \frac{\tanh(x) + \tanh(y)}{1 + \tanh(x)\tanh(y)}.
\end{align*}- \cosh(x-y) = \cosh(x)\cosh(y) - \sinh(x)\sinh(y)
- \sinh(x-y) = \sinh(x)\cosh(y) + \cosh(x)\sinh(y)
- \tanh(x - y) = \frac{\tanh(x) - \tanh(y)}{1 - \tanh(x)\tanh(y)}.
Proof 1. We first start with \cosh(x-y) = \cosh(x)\cosh(y) - \sinh(x)\sinh(y):
\begin{align*}
\cosh(x)\cosh(y) - \sinh(x)\sinh(y) &= \frac{e^x + e^{-x}}{2} \cdot \frac{e^y + e^{-y}}{2} - \frac{e^x - e^{-x}}{2}\cdot \frac{e^y - e^{-y}}{2} \\
&= \frac{1}{4}(e^{x+y} + e^{x - y} + e^{-x + y} + e^{-x-y}) \ - \\ & \ \quad \frac{1}{4}(e^{x+y} - e^{x - y} - e^{-x + y} + e^{-x-y}) \\
&= \frac{1}{2}(e^{x - y} + e^{-(x-y)}) \\
&= \cosh(x - y)
\end{align*}\begin{align*}
\sinh(x)\cosh(y) - \cosh(x)\sinh(y) &= \frac{e^x - e^{-x}}{2} \cdot \frac{e^y + e^{-y}}{2} - \frac{e^x + e^{-x}}{2}\cdot \frac{e^y - e^{-y}}{2} \\
&= \frac{1}{4}(e^{x+y} + e^{x - y} - e^{-x + y} - e^{-x-y}) \ - \\ & \ \quad \frac{1}{4}(e^{x+y} - e^{x - y} + e^{-x + y} - e^{-x-y}) \\
&= \frac{1}{2}(e^{x - y} - e^{-(x-y)}) \\
&= \sinh(x-y)
\end{align*}\begin{align*}
\tanh(x - y) &= \frac{\sinh(x - y)}{\cosh(x - y)} \\
&= \frac{\sinh(x)\cosh(y) - \cosh(x)\sinh(y)}{\cosh(x)\cosh(y) - \sinh(x)\sinh(y)} \\
&= \frac{\sinh(x)\cosh(y) - \cosh(x)\sinh(y)}{\cosh(x)\cosh(y) - \sinh(x)\sinh(y)} \cdot \frac{\frac{1}{\cosh(x)\cosh(y)}}{\frac{1}{\cosh(x)\cosh(y)}} \\
&= \frac{\frac{\sinh(x)\cosh(y)}{\cosh(x)\cosh(y)} - \frac{\cosh(x)\sinh(y)}{\cosh(x)\cosh(y)}}{\frac{\cosh(x)\cosh(y)}{\cosh(x)\cosh(y)} - \frac{\sinh(x)\sinh(y)}{\cosh(x)\cosh(y)}} \\
&= \frac{\frac{\sinh(x)}{\cosh(x)} - \frac{\sinh(y)}{\cosh(y)}}{1 - \frac{\sinh(x)}{\cosh(x)}\cdot\frac{\sinh(y)}{\cosh(y)}} \\
&= \frac{\tanh(x) - \tanh(y)}{1 - \tanh(x)\tanh(y)}.
\end{align*}